
어제의 적(skyrmion annihilation)은 오늘의 동료
어제의 적(skyrmion annihilation)은 오늘의 동료
앞선 연구[M. Song et al., Applied Physics Express 13, 063002 (2020)]에서는 자구벽을 이용해 스커미온의 소멸을 방지하고자 했습니다. 그러나 본 연구에서는, 최초로 스커미온의 소멸을 역이용할 수 있는 아이디어를 제안합니다. 메모리 소자에서는 스커미온이 보존되어야 하지만, 논리 소자에서는 입출력 시에 1과 0의 개수가 보존되는 것이 오히려 연산 기능을 저해합니다. 스커미온이 물리적 경계에서 소멸하는 조건이 분석되었기 때문에[1], 이로써 스커미온의 소멸을 선택적으로 조절하여, 덧셈 연산을 할 수 있는 가산기(adder) 소자를 구현했고, 시뮬레이션을 통해 증명했습니다.
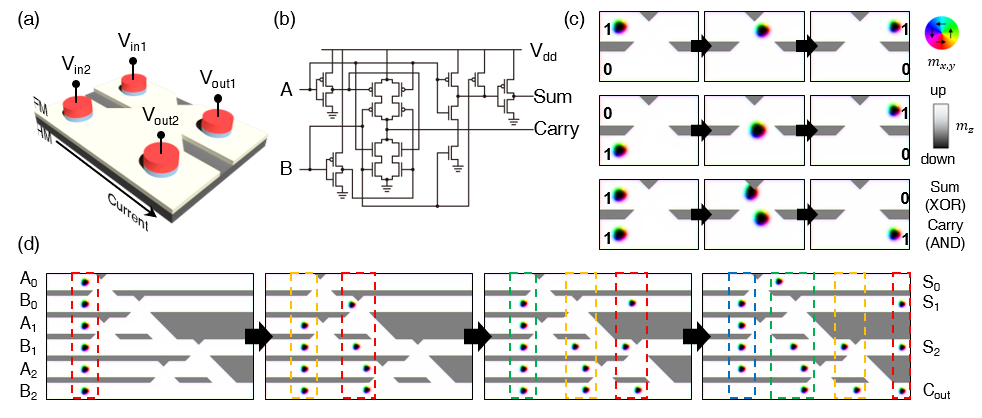
그림 1 스커미온 소멸을 이용한 논리 소자 (SA logic gate). (a) SA 반가산기 소자의 구조도. MTJ (Magnetic Tunnel Junction)로 이루어진 입출력 단자와 강자성체/중금속 이중층으로 이루어진 연산 부분(스커미온 진행 부분)으로 구성된다. (b) 기존 CMOS 기반 반가산기 회로도. 18개의 트랜지스터로 구성되나, 그 기능은 (a)와 동일하다. (c) SA 반가산기의 동작 과정. (d) 3-bit SA 가산기의 병렬 컴퓨팅 동작 과정. 빨강, 노랑, 초록, 파랑의 점선 상자로 표시된 입력 그룹이 순서대로 연산 처리된다.
그림 1(c)는 제가 제안한 SA (Skyrmion Annihilation) 반가산기의 작동 과정을 나타냅니다. 왼쪽의 두 입력 단자에 스커미온이 생성되면, 왼쪽에서 오른쪽으로 흐르는 전류에 의해 스커미온이 이동합니다. SOT와 스커미온 홀 효과에 의해 스커미온은 우상향으로 움직이려는 힘을 받는데, 입력이 (1,1)일 때(위에서 세 번째 그림)는 중앙에서 두 스커미온이 서로 반발합니다[2]. 이 때, 위쪽에 설치된 삼각형 노치(notch)에 의해서 위쪽 스커미온만이 소멸되고, 경사진 물리적 경계와의 반발력으로 남은 스커미온이 아래쪽 출력 단자로 내려옵니다. 결과적으로 위쪽 출력 단자는 XOR, 아래쪽 출력 단자는 AND 게이트 연산의 출력을 나타내게 되고, 이는 1비트 덧셈의 기능을 하는 반가산기 소자에 해당합니다. 이 SA 반가산기를 직접적으로 결합하여 SA 전가산기(full adder)를 구현했고, 나아가 1개의 반가산기와 (n-1)개의 전가산기를 연결한 임의의 n비트 가산기 소자의 구현이 가능함을 보였습니다. 그림 1(d)는 3비트 가산기의 동작을 보여주는데, 3비트 수의 덧셈을 수행할 수 있을 뿐 아니라 일정 간격으로 생성된 입력을 동시에 처리하는 병렬 연산이 가능합니다. 그림에서 보여주고 있는 것은 7+7, 6+6, 6+7, 6+3을 동시에 수행하는 과정입니다.
제안된 SA 논리 게이트의 가장 큰 장점은 구조적 단순함입니다. 기존 스커미온 논리 소자로는[2-5] AND, OR과 같은 기본 논리 게이트만이 제안되었기 때문에, 가산기와 같이 복잡한 기능의 소자를 구현하기 위해서는 기본 논리 게이트를 복합적으로 연결해 거대한 회로를 구성해야만 했습니다(그림 1(b)). 그러나 본 연구의 SA gate는 단순한 구조(그림 1(a))를 갖는 단 하나의 소자만으로 가산기 소자를 구현할 수 있습니다. 이는 소비 전력 측면에서도 큰 이득이 되는데, 32 비트 가산기 소자의 소비 에너지를 계산해본 결과 기존 스커미온 논리 게이트 대비 약 18% 수준의 에너지를 사용하는 것으로 나타났습니다.
본 연구를 요약하면, 가장 근본적인 영역에 있는 지식인 ‘위상학’을 ‘덧셈을 구현하는 컴퓨팅 소자’로 연결, 즉 ‘위상학 컴퓨터’를 만들었다고 할 수 있습니다. 이 ‘위상학 컴퓨터’는 기존의 컴퓨터의 작동 방식과는 전혀 다른 것이어서, 구조와 에너지 측면에서 향상된 성능을 낼 수 있습니다. 잘 알려진 ‘무어의 법칙’에 따르면, 매년 집적회로에 들어가는 트랜지스터의 수가 2배로 증가한다고 합니다. 한편, SA 논리 게이트는 그림 1(a)와 그림 1(b)의 비교에서 알 수 있듯 기존 트랜지스터 기반 소자와 그 궤를 달리하는 수준의 단순한 구조를 가집니다. 따라서 본 연구에는 스커미온의 위상학적 특성을 논리 소자로 응용했다는 의미가 있음과 동시에, 기존 전자 소자의 경향을 뛰어넘은 새로운 소자의 시작을 제안했다는 의미가 있습니다.
References
[1] M.-W. Yoo, V. Cros, and J.-V. Kim, Physical Review B 95, 184423 (2017).
[2] S. Luo, M. Song, X. Li, Y. Zhang, J. Hong, X. Yang, X. Zou, N. Xu, and L. You, Nano Lett 18, 1180 (2018).
[3] X. Zhang, M. Ezawa, and Y. Zhou, Scientific Reports 5, 9400 (2015).
[4] M. G. Mankalale, Z. Zhao, J.-P. Wang, and S. S. Sapatnekar, IEEE Transactions on Electron Devices 66, 1990 (2019).
[5] Z. Zhang, Y. Zhu, Y. Zhang, K. Zhang, J. Nan, Z. Zheng, Y. Zhang, and W. Zhao, IEEE Electron Device Letters 40, 1984 (2019).
- 저자의 말 -
- 저자의 말 -
Skyrmion이 서 말이라도 꿰어야 보배
Skyrmion이 서 말이라도 꿰어야 보배
여지껏 해 오던 skyrmion에 대한 시뮬레이션 연구의 방향을 살짝 틀어서, 이번에는 전통적인 전자공학 소자 저널인 IEEE Transactions on Electron Devices에 논문을 실어 보았습니다.
‘구슬이 서 말이라도 꿰어야 보배’라는 말이 있습니다. 아무리 예쁜 것을 잘 빚어내도 쓸모가 없으면 별 의미가 없다는 뜻이겠지요. 연구를 하면서도 그런 생각을 참 많이 합니다. 물리학적으로 아무리 아름답더라도, 그게 우리 세상에 영원히 나오지 못할 것이라면 그건 한낮 학자들의 여흥거리에 불과한 것이 아닌가 생각하곤 합니다.
물론 공학 분야의 연구를 보다 보면 소위 ‘공돌이들이 갈려 나간’, 물리학적으로 의미가 없어 보이는 ‘노가다’ 연구들도 더러 보입니다. 결국 학문적 의미와 실용적 가치 사이에서 균형을 잘 잡아야 하겠지요. 그런 측면에서 응용물리학이라는 분야는 참 적절한 분야이지 않나 생각합니다. 말 그대로 응용이면서, 물리학이니까요. 그러나 뒤집어 보면, 공학과 과학 어디에도 분류할 수 없는 애매한 분야라고도 할 수 있겠습니다.
학회에서 이번 연구를 발표하면서 이런 이야기를 했습니다. “‘로직 소자를 만들었으니 컴퓨팅을 할 수 있다’고 말하는 것은, ‘여기 밀가루가 있으니 빵을 먹을 수 있다’고 말하는 것과 같다.” 빵을 만들기 위해서는 밀가루뿐만 아니라 다양한 재료와 레시피, 그리고 요리사의 솜씨가 필요한데, 우리 분야에는 말하자면 ‘밀의 수확 방법’에 대해 연구하고서 ‘우리는 이제 빵을 먹을 수 있다!’고 이야기하는 경우가 꽤 많습니다. 저는 참 의아했습니다. 왜 아무도 밀 -> 빵으로 가는 중간 과정을 궁금해하지 않는 것일까? 다들 시도는 해 보고서 말하는 걸까? 안 되는 걸 아는데 거짓말을 하는 걸까, 아니면 정말로 해봤는데 가능성이 보여서 저런 말을 하는 걸까? 실제로 많은 응용물리학 연구자들이 ‘아이디어를 내면 공학 하는 사람이 어떻게든 실제로 만들어 내겠지’라는 마음가짐을 갖고 연구를 하는 것 같습니다. 그런데 저는 이것이 왠지 찝찝하게 느껴졌습니다. 제가 하고 있는 연구가 얼마나 실현 가능성이 있는지를 그냥 남에게 맡기는 것이 아닌, 직접 알아보고 싶었습니다. 그래서 물리를 하는 사람으로서 흔치 않게, ‘소자를 만드는 연구’에 관심을 가져 보았습니다.
연구 아이디어를 만들어 준 건 학부생 때 수강했던 전자과 디지털시스템 과목이었습니다. 당시 강의를 들으며 0과 1, AND, OR과 같은 개념으로 덧셈, 뺄셈, 곱셈을 다 할 수 있다는 게 참 신기했습니다. 돌이켜 보면, ‘1+1=2‘와 같이 일상적으로 당연하다고 생각하는 개념들을 0과 1로 작동하는 컴퓨터에 이식시키는 방법, 즉 ‘계산’에 대한 공학적 사고를 배울 수 있었던 것 같습니다. 이후 대학원에 진학해 연구를 하다 보니, 물리학을 하는 사람들이 skyrmion을 연구하면서 ‘이걸로 메모리도 만들 수 있고, 컴퓨터도 만들 수 있다’고들 말하는데, 정작 skyrmion으로 덧셈이 되는 걸 보인 사람은 여지껏 아무도 없었다는 게 눈에 띄었습니다. 덧셈 소자 만드는 법은 전자과 2학년 과목에도 나오는데 말이지요. “그래? 그럼 내가 하지.” 기존의 skyrmion 로직 소자 관련 논문들과 디지털시스템 교재를 양 옆으로 두고 이리저리 고민해 보았습니다. 그러다 문득 방법을 찾아냈습니다. “skyrmion이 없어지면 되잖아?”
‘skyrmion이 없어지면 된다’는 개념은 말하자면 물리학에서 ‘금지된’ 개념이었습니다. 왜냐하면 skyrmion이라는 입자는 그 보존성이 수학적으로 증명된 입자이기 때문입니다. 거기에는 topology라는 강력한 물리학적 개념이 있어서, skyrmion은 topology가 보호해주는(실제로 topologically protected라는 말을 쓰듯) 존재로 여겨져 왔습니다. 그런데 최근 몇 년 간 전 세계 수많은 연구진들이 실험으로 확인해 본 결과, skyrmion이 이론과는 달리 일상적인 수준의 작은 자극에도 잘 없어진다는 것이 관측되었습니다. 현실이 수학을 배반했다고 볼 수 있겠지요. 이 현상을 단순히 이론과 실제의 괴리로 치부할 것인지, skyrmion topology 이론에 대한 해석 방식을 뜯어고쳐야 할 것인지는 아직 불확실합니다. 그러나 어찌되었건, 현실에서 없어진다는 건 변치 않는 사실입니다. 알 수 없는 소멸 현상, ‘피할 수 없다면 이용하자’고 저는 생각했습니다. 남들이 받아들이지 않던 skyrmion의 소멸을 당연한 것으로 받아들이자 문제가 풀리지 시작했습니다. 여기에 디지털시스템 과목에서 배운 로직 소자 개념을 접목시키자 지금까지 없던 소자 디자인이 나왔고, 이를 시뮬레이션으로 구현해 skyrmion으로 덧셈 계산을 할 수 있다는 걸 보였습니다.
이 결과만으로 ‘skyrmion으로 컴퓨터를 만들 수 있다!’라고 말하기에는 한참 모자랍니다. 그러나 물리학의 영역에 있던 skyrmion을 전자공학, 전자 소자 디자인의 영역으로 조금이나마 밀어내 보려고 했던 노력은 나름 의미가 있다고 생각합니다. 밀을 많이 수확해 놓고 올해는 빵을 많이 먹겠다며 만족하는 것과, 그것을 가져다 빵을 만들려 시도한 것은 완전히 다른 자세인 것처럼요. 어쩌면 그런 자세에 대해 끊임없이 생각하는 것이 물리학과 공학 사이에 낀 응용물리학자가 짊어져야 할 과제일 지도 모릅니다. 그런 생각을 하며 ‘내가 해야 할 연구는 무엇인가’, ‘우리 분야는 대체 어떻게 될 것인가’ 등 학문의 변천과 그 속의 연구자로서의 제 자신에 대해 이모저모로 생각해 보게 되었는데, 그런 점에서 이번 연구는 개인적으로 꽤나 큰 의미가 있었습니다.
‘구슬이 서 말이라도 꿰어야 보배’라지만, 구슬을 예쁘게 잘 빚어내는 사람이 있는가 하면 구슬을 잘 꿰는 사람도 있습니다. 무엇을 해야 한다는 데에 정해진 답이 있지는 않고, 그냥 자기가 잘 하는 것, 하다 보면 즐거운 것을 하면 그만이라 생각합니다. 개중에는 ‘구슬에 구멍 뚫는 사람’도 있을 것인데, 그게 말하자면 응용물리학자의 모습이지 않을까요. 그런 틈새를 파는 일들이 즐겁고, 또 계속 할 수 있다는 게 참으로 감사합니다. 앞으로도 이리 저리 머리를 잘 굴려서, 제가 할 수 있는 일들을 잘 해 봐야겠습니다. 요즘은 이론보다는 실험을 주로 하고 있는데, 정말로 이론 속 서 말의 skyrmion에 구멍을 잘 뚫어내는, 나아가 보배로 만들 수 있는 날이 온다면 좋겠습니다.
저자 송무준
E-mail : [email protected]
To cite this article:
M. Song et al., IEEE Trans. Electron Devices 68, 1939 (2021)
DOI:
https://doi.org/10.1109/TED.2021.3055157