Seminar/Article Journal club
Néel-type skyrmion in WTe2/Fe3GeTe2 van der Waals heterostructure
Néel-type skyrmion in WTe2/Fe3GeTe2 van der Waals heterostructure
Mermin-Wagner Theorem[1]에 의하면 2D 이하의 차원에서 long range magnetic ordering이 불가능하다. 즉, 우리가 흔히 사용하는 강자성체인 Co, Permalloy, CoFeB같은 3D Heisenberg ferromagnet이 Monolayer limit으로 내려가게 되면 강자성 특성이 나오지 않음을 의미한다. 하지만 이러한 low dimension에서도 강력한 magnetic anisotropy가 존재한다면 monolayer limit에서도 강자성 특성이 나올 수 있는데, 최근 많이 연구가 되고 있는 물질이 바로 van der Waals 물질이다. 비슷한 시기에 CrI3라는 물질과[2] Cr2Ge2Te6[3], Fe3GeTe2[4] 등의 van der Waals 물질에서 강자성 특성을 실험적으로 확인하였다. 그 뒤로 기존의 3D Heisenberg ferromagnet에서 하던 여러 연구들이 2D에 적용되어 활발하게 진행되고 있다[5, 6, 7]. 본 논문에선 Fe3GeTe2(FGT) 물질에서 magnetic skyrmion을 Lorentz TEM(L-TEM)으로 확인하고, skyrmion으로 인한 topological Hall effect를 전기적으로 확인하였다.
이 논문에서 주장하는 것은 WTe2와 FGT 사이의 interfacial Dzyaloshinskii-Moriya interaction(DMI)으로 인하여 FGT에 Néel-type skyrmion이 생성된다는 것이다. 그 주장의 근거 중 하나는 바로 topological Hall effect(THE)이다. THE는 간단히 요약하면 ‘Spin chirality driven Hall response’로 말할 수 있다. 즉, 전자가 이동하는 중에 magnetic skyrmion과 같은 chiral spin texture를 만나면 자신이 가지고 있는 스핀에 따라 additional phase가 생기게 되고, 그것이 Hall response로 관측되는 것이다. 아래 그림이 이를 보여준다.
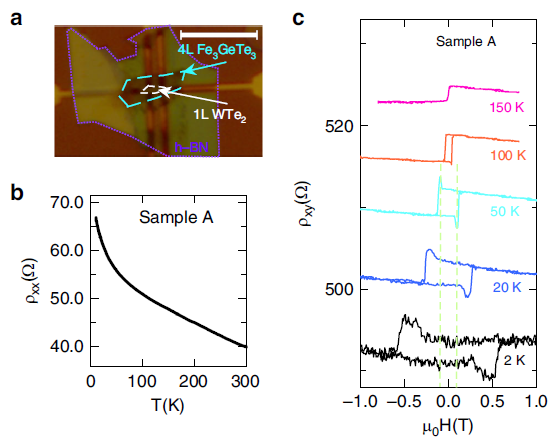
위의 그림은 본 논문의 Fig. 1의 데이터 중 일부이다. (c)는 4 layers FGT 위에 1 layer WTe2가 있는 구조에서 out of plane 방향으로 field sweep을 하여 anomalous Hall signal을 측정한 것이다. 데이터에서 볼 수 있듯이 온도가 낮은 구간에서 자화가 up에서 down으로 변하는 지점에 dip과 peak이 존재함을 알 수 있다. 이는 적절한 field 구간에서 anomalous Hall signal 이외에 다른 Hall signal이 묻어나온다는 것인데, 이 추가적인 신호가 magnetic skyrmion에 의한 topological Hall signal이라는 것이다. 그래서 본 논문에선 실제로 magnetic skyrmion을 관측하기 위해 L-TEM을 이용하였고, 그 결과는 아래 그림과 같다.
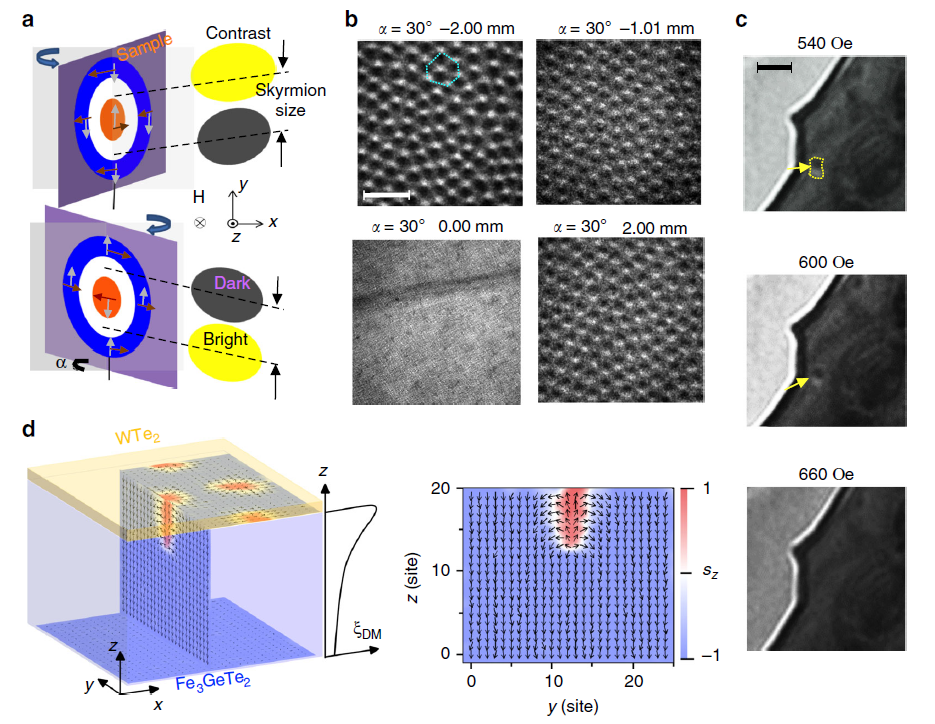
L-TEM에선 원리상 Néel-type skyrmion을 찍을 수 없어서 샘플과 입사 전자 사이의 각도를 약간 조절하여 이미징 한다(a). 그렇게 하여 임의로 샘플을 투과하는 전자들의 경로 차이를 만들어 결과적으로 명암차이를 만들고, 이를 이용하여 skyrmion을 이미징 하는 것이다(b, c). 이로써 실제로 이 구조에서 interfacial DMI로 인한 Néel-type skyrmion이 생성됨을 증명하였다. 추가적으로 skyrmion이 FGT와 WTe2의 계면 가까이에서 생긴다는 것을 시뮬레이션을 통하여 보였다(d).
그렇다면 이 interfacial DMI의 크기는 어느정도 될까? 이를 알기 위하여 본 논문에선 domain wall width를 분석하였다. Domain wall width는 domain의 에너지에 비례를 하는데, DMI의 유무에 따라 이 domain wall의 에너지가 달라진다. Domain wall width(w)와 domain energy(δw)는 다음과 같이 쓸 수 있다.
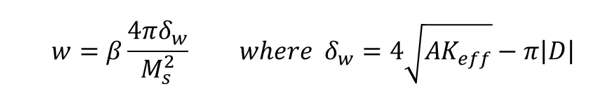
여기서 A는 exchange stiffness, Keff는 effective anisotropy constant, Ms는 saturation magnetization, D는 DMI constant이다. 만약 DMI가 있을 때와 없을 때의 domain wall width를 알 수 있으면, D를 유추할 수 있다.
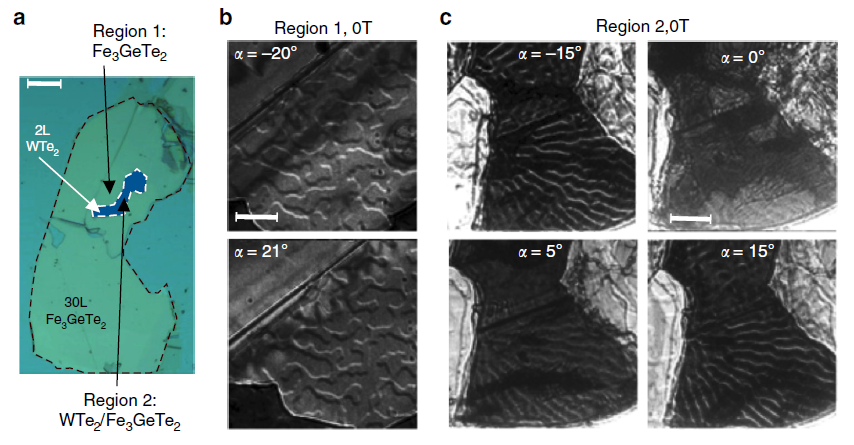
위 그림과 같이 FGT 위에 WTe2가 있는 영역(c)과 없는 영역(b)에서의 domain wall width를 이용하여 D의 값을 계산하였고, 1.0 mJ/m2의 값이 나왔다고 한다. 기존의 보고들에 비하면 굉장히 큰 DMI constant를 갖고 있다.
References
[1] Phys. Rev. Lett. 17, 1307 (1966)
[2] Nature 546, 270 (2017)
[3] Nature 546, 265 (2017)
[4] Nat. Mater. 17 778 (2018)
[5] Nature 563, 94 (2018)
[6] Nat. Phys. 17, 20 (2021)
[7] Science Advances 5, eaaw8904 (2019)
작성 지유빈
E-mail : [email protected]
참석자(ZOOM seminar): 박민규, 원운재, 박재현, 이택현, 이근희, 유무진, 송무준, 양지석, 지유빈, 고산, 장유준
DOI:
https://doi.org/10.1038/s41467-020-17566-x